Introduction to Combinatorial Optimization

2023-02-07

9 min read

Reinforcement Learning for Combinatorial Optimization

Provide a brief and basic overview of Operations Research (OR) and Combinatorial Optimization (CO) concepts that are essential for understanding the application of Reinforcement Learning for Operation Research.

In early 2022, I made a survey about the frontier of Reinforcement Learning (RL) in Operations Research (OR). As an AI researcher, I was interested in the application of RL in solving complex optimization problems and tried to figure out if there is any possible work that I can contribute. Through my survey, I gained somehow an understanding of the state-of-the-art in this field. Although I eventually shifted my focus to other areas, I hereby would like to share my insights and possibly facilitate future research. I hope this series of blog posts could provide a comprehensive overview of RL4OR for those who come after me.

What is Operating Research (OR)

At the beginning of my survey, I tried to search and understand what exactly Operating Research is:

Operations Research (OR) is a branch of mathematics that deals with the application of scientific methods, mathematical models, and algorithms to decision making problems in real-world operations.

During my research, I discovered that defining the exact nature of operations research is challenging, and organizing its research into structured chapters is equally difficult compared to other disciplines. This is not surprising given that operations research originated from military applications prior to World War II, and its primary objective is to utilize mathematical techniques to achieve optimal or near-optimal solutions for decision-making problems.

Therefore, I attempted to approach the subject by categorizing it according to its practical applications. According to Wikipedia, the major sub-disciplines in modern operational research are:

|- Computing and information technologies
|- Financial engineering
|- Manufacturing, service sciences, and supply chain management
|- Policy modeling and public sector work
|- Revenue management
|- Simulation
|- Stochastic models
|- Transportation theory (mathematics)
|- Game theory for strategies
|- Linear programming
|- Nonlinear programming
|- Integer programming in NP-complete problem specially for 0-1 integer(linear programming for binary)
|- Dynamic programming in Aerospace engineering and Economics
|- Information theory used in Cryptography, Quantum computing
|- Quadratic programming for solutions of Quadratic equation and Quadratic function

In my view, these sub-disciplines often intersect with one another, and as operations research continues to develop and evolve, the list of sub-disciplines keeps expanding. I believe this list cannot provide a precise description of operations research as a whole.

At the same time, another related concept caught my attention, i.e. Combinatorial Optimization (CO), which is increasingly used by researchers as a preferred terminology over operations research in papers.

Combinatorial Optimization (CO)

For some of us, it may be more familiar to discuss Combinatorial Optimization (CO), a subfield of mathematical optimization that consists of finding an optimal object from a finite set of objects, where the set of feasible solutions is discrete or can be reduced to a discrete set.

Specific problems in Combinatorial Optimization can be roughly categorized as:

- Assignment Problems:
    - Assignment problem
    - Generalized assignment problem
    - Quadratic assignment problem
    - Weapon target assignment problem
    - Resource allocation problems
- Closure problem
- Constraint satisfaction problem
- Cutting stock problem: Cutting small items out of bigger ones.
- Dominating set problem
- Integer programming
- Bin packing problem
    - Knapsack problem
    - Floorplanning: designing the layout of equipment in a factory or components on a computer chip to reduce manufacturing time (therefore reducing cost)
- Minimum relevant variables in linear system
- Minimum spanning tree
- Set cover problem: for instance, facility location problem or a network optimization problem (such as setup of telecommunications or power system networks to maintain quality of service during outages)
- Scheduling:
    - Personnel staffing
    - Manufacturing steps
    - Project tasks
    - Network data traffic: these are known as queueing models or queueing systems.
    - Sports events and their television coverage
    - Job shop scheduling
- Routing
    - Traveling salesman problem
    - Vehicle rescheduling problem
    - Vehicle routing problem

Each of these problems has its unique characteristics, but they share the common feature of being discrete optimization problems. Due to my limited survey time, I focused my research on a subset of the aforementioned Combinatorial Optimization problems.

Routing Problems

As one of the most frequently encountered optimization tasks, vehicle routing aims to determine the best routes for a fleet of vehicles to visit a specific set of locations. Usually, “best” means routes with the least total distance or cost. Here are a few examples of routing problems:

A package delivery company wants to assign routes for drivers to make deliveries.
A cable TV company wants to assign routes for technicians to make residential service calls.
A ride-sharing company wants to assign routes for drivers to pick up and drop off passengers.¹

Traveling Salesman Problem (TSP)

The most famous routing problem is the Traveling Salesperson Problem (TSP): find the shortest route for a salesperson who needs to visit customers at different locations and return to the starting point.

Definition Traveling Salesman Problem (TSP): Given a complete weighted graph $𝐺 = (𝑉, 𝐸)$, find a tour of minimum total weight, i.e. a cycle of minimum length that visits each node of the graph exactly once.

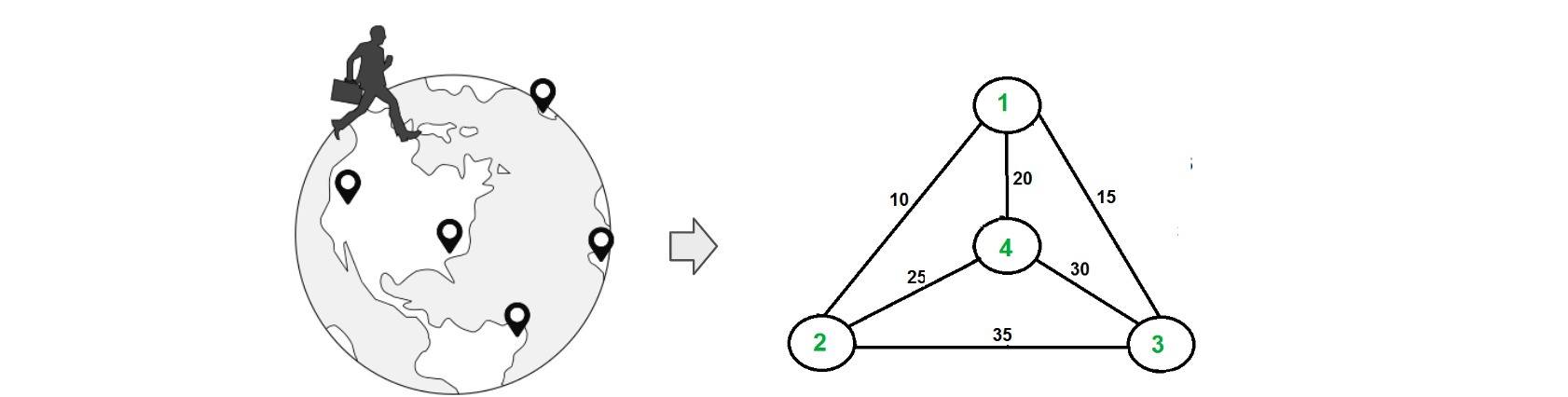
The Traveling Salesman Problem (TSP) has numerous applications in various industries. Some examples include:

Logistics and transportation: TSP can be used to optimize the routes of delivery vehicles, reducing transportation costs and improving efficiency.
Chip manufacturing: TSP can be used to optimize the path of a machine that drills holes in a silicon wafer, reducing production time and increasing efficiency.
Network routing: TSP can be used to optimize the routing of data packets in a computer network, reducing latency and improving performance.
DNA sequencing: TSP can be used to determine the optimal order for sequencing DNA fragments, reducing the cost and time required for DNA sequencing.


Food Delivery Route Planning	Chip Design	Power Grid Design


DNA Sequencing

For people interested in further research on the Traveling Salesman Problem, Chaitanya K. Joshi’s blog can be a valuable resource to explore.

Packing Problems

The goal of packing problems is to find the best way to pack a set of items of given sizes into containers with fixed capacities. A typical application is loading boxes onto delivery trucks efficiently. Often, it’s not possible to pack all the items, due to the capacity constraints. In that case, the problem is to find a subset of the items with maximum total size that will fit in the containers.¹


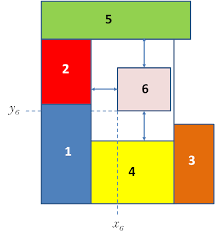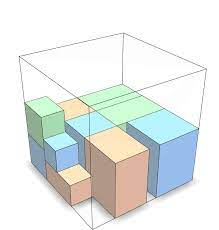2D Packing	3D Packing

There are many types of packing problems. Two of the most important are knapsack problems and bin packing. Definition Knapsack Problem: Given a set $S$ of $n$ items, each with a weight $w_i$ and a value $v_i$, and a knapsack that can hold a maximum weight $W$, the goal is to find a subset $S’ \subseteq S$ that maximizes the total value of the items in $S’$, subject to the constraint that the total weight of the items in $S’$ does not exceed $W$.

\[\begin{align} \max_{S' \subseteq S} & \sum_{i \in S'} v_i\ \text{s.t. } & \sum_{i \in S'} w_i \leq W. \end{align}\]

Definition Bin Packing Problem (BPP): Given a set $S$ of $n$ items, each with a size $s_i$ and a set of $m$ bins, each with a capacity $C$, the goal is to pack all the items into the minimum number of bins, subject to the constraint that the total size of the items in each bin does not exceed the bin’s capacity.

\[\begin{equation} \begin{split} \min_{x_{ij} \in {0,1}} & \sum_{i=1}^{n} \sum_{j=1}^{m} x_{ij}\\ \text{s.t. } & \sum_{i=1}^{n} s_i x_{ij} \leq C \quad \text{for } j=1,2,\dots,m\\ & \sum_{j=1}^{m} x_{ij} = 1 \quad \text{for } i=1,2,\dots,n \end{split} \end{equation}\]

We can also observe a lot of applications of packing problems, some examples are:

Container loading: Determining the optimal way to load items into shipping containers to maximize space utilization and minimize shipping costs.
Material cut planning: Optimizing the use of materials during manufacturing
Task assignment in servers: Maximizing server efficiency and energy consumption in server farms
Online voucher distribution: Determining the most effective method for distributing vouchers in online shopping platforms


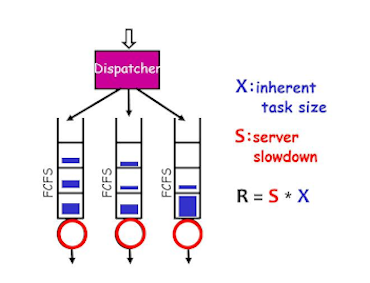Container Loading	Material Cutting Plan	Task Assignment in Server Farm


Voucher Distribution

Assignment Problems

The assignment problem is a fundamental combinatorial optimization problem.

In its most general form, the problem is as follows:
The problem instance has a number of workers and a number of tasks. Any worker can be assigned to perform any task, incurring some cost that may vary depending on the agent-task assignment. It is required to perform as many tasks as possible by assigning at most one worker to each task and at most one task to each agent, in such a way that the total cost of the assignment is minimized.

Alternatively, describing the problem using graph theory:
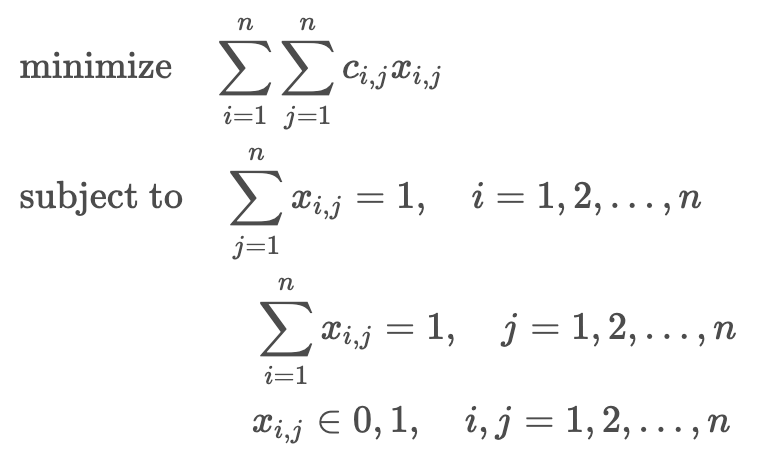
The assignment problem consists of finding, in a weighted bipartite graph, a matching of a given size, in which the sum of weights of the edges is minimum.

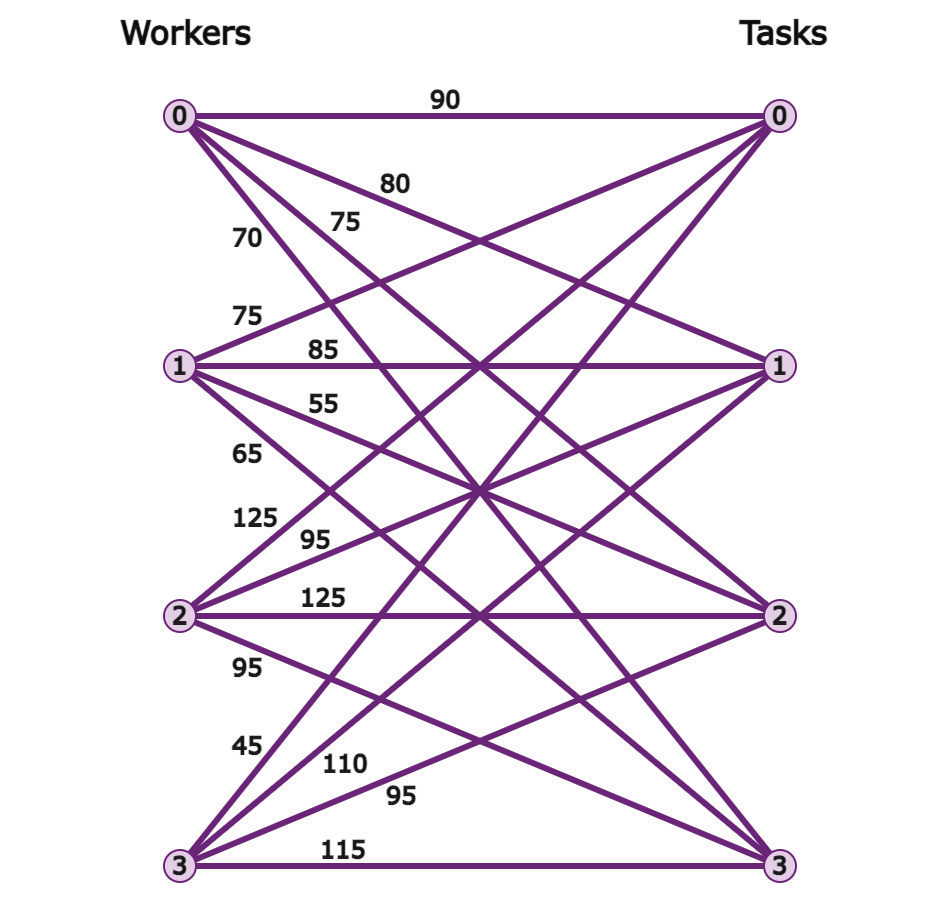
Mixed-Integer Program (MIP)

Combinatorial optimization problems come in many different forms and categories. However, upon closer examination, it becomes clear that many of these problems can be transformed into one another. For instance, the knapsack problem and the assignment problem are interconnected as the former can be viewed as the latter by considering the assignment of an item to a knapsack as equivalent to putting the item into the knapsack.

Among those, Mixed Integer Linear Programs (MIPs) offer a generic way of formulating and solving combinatorial optimization problems. According to (Conforti et al., 2014) ², any combinatorial optimization problem with finite feasible region can be formulated as a MIP instance.

Definition Mixed-Integer Program (MIP)

\[\begin{equation} \begin{split} \text{minimize} &\quad c^T x \\ \text{subject to} &\quad Ax \leq b \\ &\quad x_i \in \mathbb{Z} \quad \text{for} \quad i \in I \\ &\quad x_j \in \mathbb{R} \quad \text{for} \quad j \in J \\ \end{split} \end{equation}\] where $c$ is the coefficient vector, $x$ is the decision variable vector, $A$ is the constraint matrix, $b$ is the constraint vector, $I$ is the set of indices for integer variables, and $J$ is the set of indices for continuous variables.

An alternative approach to representing MIP problems is through the use of a bipartite graph: Graph Representation of MIPs

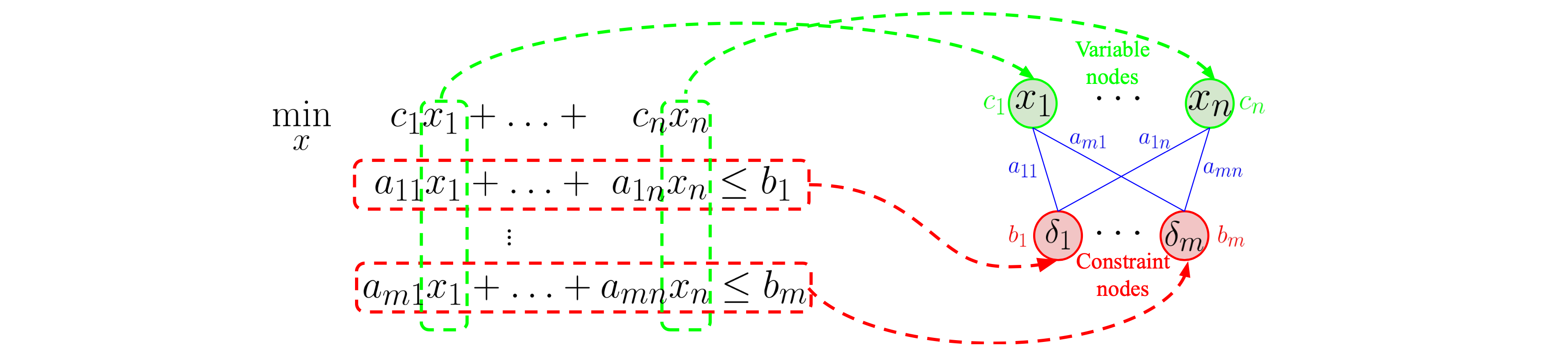
Graph Representation of MIPs was first proposed in (Gasse et al., 2019) ³ and can be used as input to a neural network as demonstrated in (Nair et al.,2020) ⁴

Graph Representation of MIPs

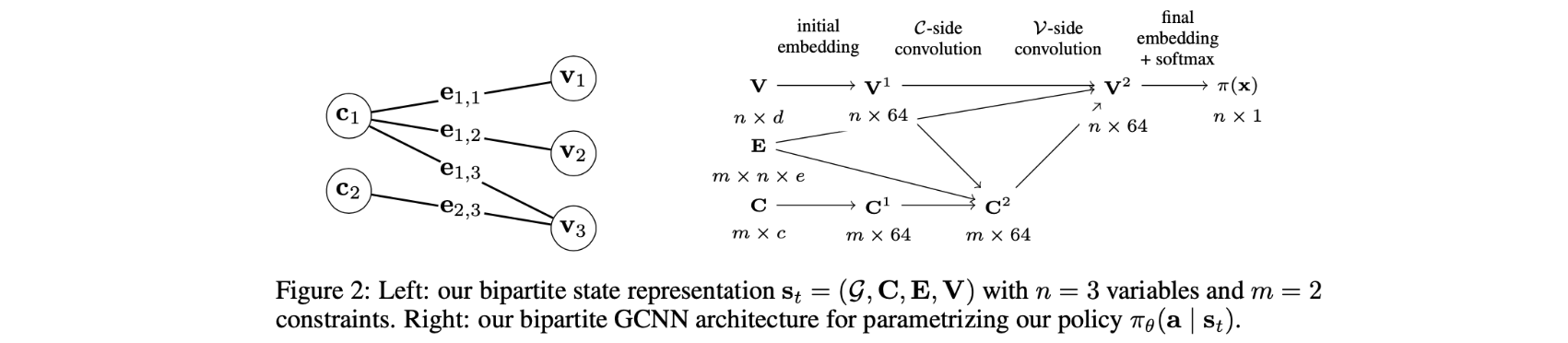
How ML/RL is used in CO

According to (Bengio et al.,2021) ⁵, the integration of learned policies, whether from demonstration or experience, with traditional combinatorial optimization (CO) algorithms was discussed from three perspectives: end-to-end learning, learning to configure algorithms, and machine learning in conjunction with optimization algorithms.

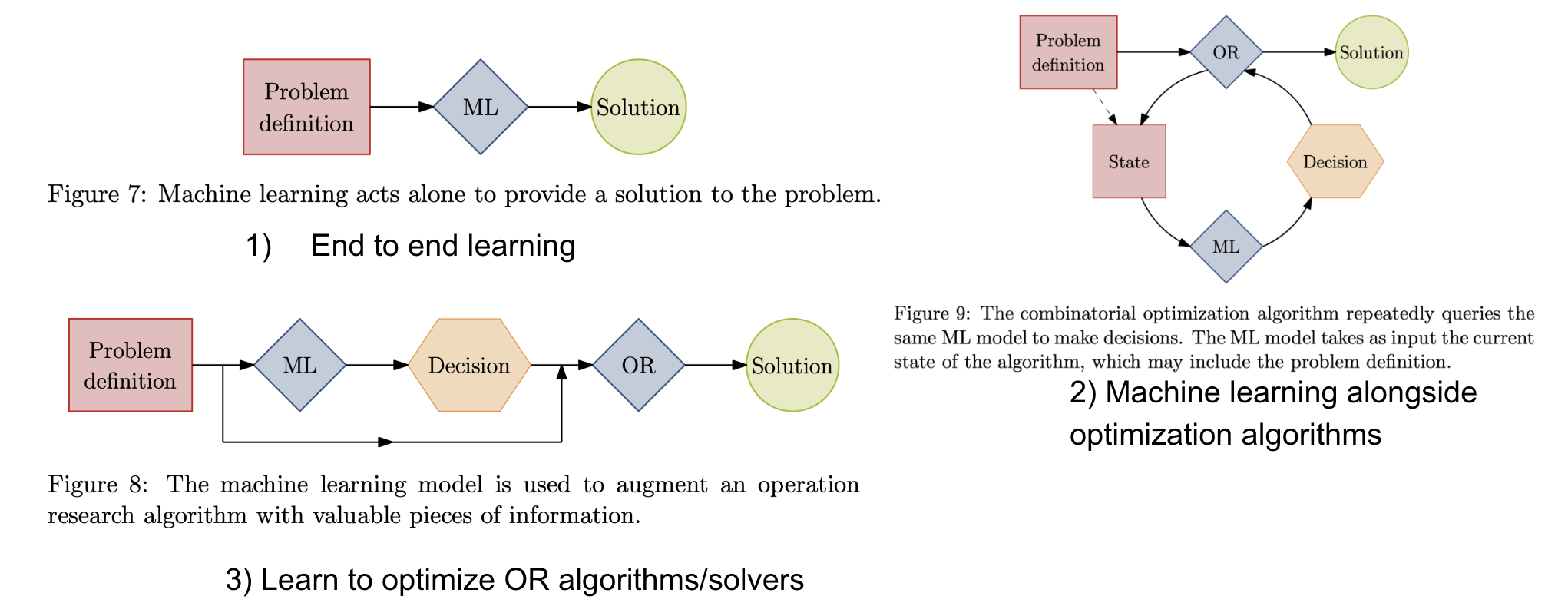In next chapter, I am going to delve into each of these three methods in more detail.

Vehicle Routing, Packing Problems by OR-Tools ↩︎ ↩︎
Conforti, Michele, et al. “Integer programming models.” Integer Programming (2014): 45-84. ↩︎
Gasse, Maxime, et al. “Exact combinatorial optimization with graph convolutional neural networks.” Advances in neural information processing systems 32 (2019). ↩︎
Nair, Vinod, et al. “Solving mixed integer programs using neural networks.” arXiv preprint arXiv:2012.13349 (2020). ↩︎
Bengio, Yoshua, Andrea Lodi, and Antoine Prouvost. “Machine learning for combinatorial optimization: a methodological tour d’horizon.” European Journal of Operational Research 290.2 (2021): 405-421. ↩︎