Table of Contents

Preliminaries #1: Diffusion Models

2023-06-05
6 min read

Overview

This blog aims to provide an intuitive introduction to Diffusion Models. For further in-depth reading, several highly recommended blogs are available:

Given observed samples $x$ from a distribution of interest, the goal of a generative model is to learn to model its true data distribution $p(x)$. Once learned, we can generate new samples from our approximate model at will. Furthermore, under some formulations, we are able to use the learned model to evaluate the likelihood of observed or sampled data as well.

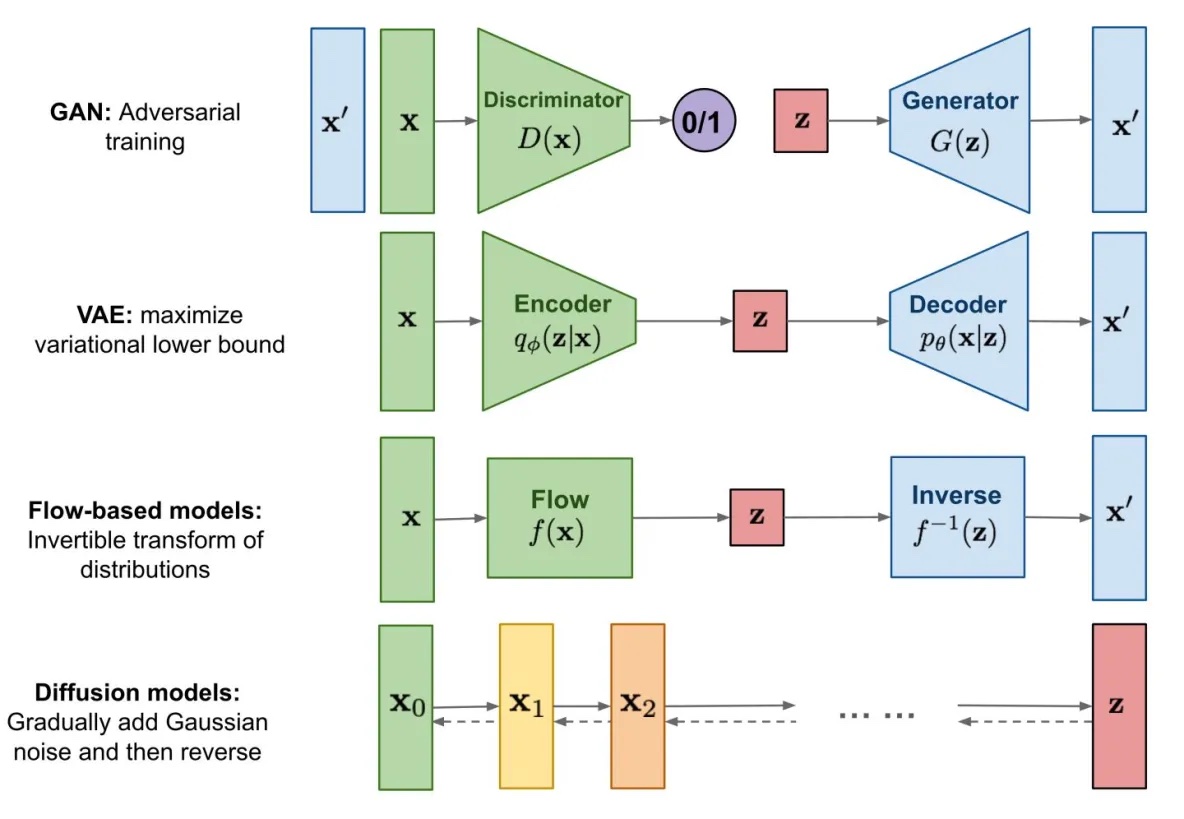
Generative Models

Background

VAE & ELBO

Before introducing Diffusion Model, let’s just revise the Variational AutoEncoder (VAE) and Evidence Lower Bound (ELBO).

Variational Autoencoder introduced a latent variable $z$ to learn the underlying latent structure that describes our observed data $x$. For training a VAE, we learn an intermediate bottlenecking distribution $q_\phi(z|x)$ that can be treated as an encoder; it transforms inputs into a distribution over possible latents. Simultaneously, we learn a deterministic function $p_\theta(x|z)$ to convert a given latent vector $z$ into an observation $x$, which can be interpreted as a decoder.

Image
Vanilla Variational Autoencoder.
A latent encoder and decoder are learned jointly through the reparameterization trick.

Mathematically, we can imagine the latent variables and the data we observe as modeled by a joint distribution $p(x, z)$. Likelihood-based generative modeling, like VAE, learns a model to maximize the likelihood $p(x)$ of all observed $x$. There are two ways we can manipulate this joint distribution to recover the likelihood of purely our observed data $p(x)$ ; we can explicitly marginalize out the latent variable $z$:

\[\begin{aligned} &p(x)= \int p(x, z)dz &(1) \end{aligned}\]
[Computing and maximizing the likelihood $p(x)$ is difficult] it involves integrating out all latent variables $z$. This is intractable for complex models.
or, we could also appeal to the chain rule of probability:
\[\begin{aligned} &p(x)=\frac{p(x, z)}{p(z|x)} &(2) \end{aligned}\]
[Computing and maximizing the likelihood $p(x)$ is difficult] it involves having access to a ground truth latent encoder $p(z|x)$.
Using these two equations, we can derive a term called the Evidence Lower Bound (ELBO).

Evidence Lower Bound (ELBO), which as its name suggests, is a lower bound of the evidence. In this case, the evidence is quantified as the log likelihood of the observed data, denoted as $\log p(x)$.

Let’s derive ELBO using the chain rule marginalization method, as in Equation 2:

\[\begin{aligned} \log p(x) &= \log p(x) \int q_\phi(z|x)dz & \small{(\int q_\phi(z|x)dz=1)}\\ &= \int q_\phi(z|x) \log p(x)dz \\ &= \mathbb{E}_{q_\phi(z|x)}\boldsymbol[ \log p(x) \boldsymbol] \\ &= \mathbb{E}_{q_\phi(z|x)}\boldsymbol[ \log \frac{p(x,z)}{p(z|x)} \boldsymbol] \\ &= \mathbb{E}_{q_\phi(z|x)}\boldsymbol[ \log \frac{p(x,z)q_\phi(z|x)}{p(z|x)q_\phi(z|x)} \boldsymbol] \\ &= \mathbb{E}_{q_\phi(z|x)}\boldsymbol[ \log \frac{p(x,z)}{q_\phi(z|x)} \boldsymbol] + \mathbb{E}_{q_\phi(z|x)}\boldsymbol[ \log \frac{q_\phi(z|x)}{p(z|x)} \boldsymbol]\\ &= \mathbb{E}_{q_\phi(z|x)}\boldsymbol[ \log \frac{p(x,z)}{q_\phi(z|x)} \boldsymbol] + \text{D}_{\text{KL}}\boldsymbol( q_\phi(z|x) \,||\, p(z|x) \boldsymbol) &\text{\small(KL definition)} \\ &\ge \underbrace{\mathbb{E}_{q_\phi(z|x)}\boldsymbol[ \log \frac{p(x,z)}{q_\phi(z|x)} \boldsymbol]}_{\text{ELBO}} &\small{(\text{D}_{\text{KL}}\text{ is non-negative)}} \end{aligned}\]
Derive ELBO using the integration marginalization and Jensen's inequality (optional)       There's an alternative method to derive ELBO from evidence, commonly found in blogs introducing Diffusion Models. However, I don't personally recommend this approach as it fails to provide sufficient intuition as to why we opt for ELBO to optimize generative models.

Jensen’s inequality states that for any concave function $f(x)$, if $X$ is a random variable, then:

\[ f(\mathbb{E}[X]) \geq \mathbb{E}[f(X)] \]

Let’s start from Equation 1, we can derive ELBO:

\[\begin{aligned} \log p(x) &= \log \int p(x, z)dz &\small{(p(x)=\int p(x, z)dz)} \\ &= \log \int \frac{p(x, z)q_\phi(z|x)}{q_\phi(z|x)} dz \\ &= \log \mathbb{E}_{q_\phi(z|x)}\boldsymbol[ \frac{p(x, z)}{q_\phi(z|x)} \boldsymbol] \\ &\ge \underbrace{\mathbb{E}_{q_\phi(z|x)}\boldsymbol[ \log \frac{p(x,z)}{q_\phi(z|x)} \boldsymbol]}_{\text{ELBO}} &\text{\small{(Jensen's inequality)}} \end{aligned}\]

      In this derivation, we directly arrive at our lower bound by applying Jensen’s Inequality. However, this does not supply us much useful information about what is actually going on underneath the hood; crucially, this proof gives no intuition on exactly why the ELBO is actually a lower bound of the evidence, as Jensen’s Inequality handwaves it away. Furthermore, simply knowing that the ELBO is truly a lower bound of the data does not really tell us why we want to maximize it as an objective.

Notice that the likelihood of our data, i.e. the evidence term $\log p(x)$, is always a constant with respect to $\phi$, as it is computed by marginalizing out all latents $z$ from the joint distribution $p(x,z)$ and does not depend on $\phi$ whatsoever. Since ELBO and KL Divergence sum up to a constant, maximizing ELBO is equivalent to minimizing KL Divergence between our approximate posterior distribution and true posterior distribution. Thus we can easily utilize ELBO as a proxy objective to optimize a latent variable model, that is, by powerfully parameterizing and perfectly optimizing the ELBO, we can make our approximate posterior $q_\phi(z|x)$ exactly equivalent to the true latent posterior $p(z|x)$.

We can rewrite ELBO into a form of VAE objective:

\[\begin{aligned} \underbrace{\mathbb{E}_{q_{\phi}(z|x)}\boldsymbol[\log \frac{p(x,z)}{q_\phi(z|x)}\boldsymbol]}_{\text{ELBO}} &= \mathbb{E}_{q_{\phi}(z|x)}\boldsymbol[\log \frac{p_\theta(x|z)p(z)}{q_\phi(z|x)}\boldsymbol]\\ &= \mathbb{E}_{q_{\phi}(z|x)}\boldsymbol[\log p_\theta(x|z)\boldsymbol] + \mathbb{E}_{q_{\phi}(z|x)}\boldsymbol[\log \frac{p(z)}{q_\phi(z|x)}\boldsymbol] \\ &= \underbrace{\mathbb{E}_{q_{\phi}(z|x)}\boldsymbol[\log p_\theta(x|z)\boldsymbol]}_{\text{reconstruction term}} - \underbrace{D_{\text{KL}}\boldsymbol(q_\phi(z|x) \,||\, p(z)\boldsymbol)}_{\text{prior matching term}} \end{aligned}\]
ELBO can be seen as a combination of two loss terms, each corresponding to a module of VAE:
  1. reconstruction term measures the reconstruction likelihood of the decoder from our variational distribution; this ensures that the learned distribution is modeling effective latents that the original data can be regenerated from.
  2. prior matching term measures how similar the learned variational distribution is to a prior belief held over latent variables. Minimizing this term encourages the encoder to actually learn a distribution rather than collapse into a Dirac delta function.
Therefore, maximizing ELBO is equivalent to approximating the true data distribution, and at the same time, optimizing the posterior latent vector distribution $q(z|x)$ using variational methods.
Variational is the term used for variational inference, a technique that approximates complex probability distributions using simpler ones. It finds the distribution in a specific class that is closest to the true posterior distribution. In VAE, it refers to the fact that we optimize for the best $q_\phi(z|x)$ amongst a family of potential posterior distributions parameterized by $\phi$.
The Dirac delta function $\delta(x)$ can be loosely thought of as a function on the real line which is zero everywhere except at the origin, where it is infinite,
\[ \delta (x)\simeq {\begin{cases}+\infty ,&x=0\\0,&x\neq 0\end{cases}} \]
and which is also constrained to satisfy the identity
\[ \int _{-\infty }^{\infty }\delta (x)\,dx=1.\]

After training a VAE, generating new data can be performed by sampling directly from the latent space and then running it through the learned decoder.

HVAE

Hierarchical Variational Autoencoder (HVAE) is a generalization of a VAE that extends to multiple hierarchies over latent variables. Under this formulation, latent variables themselves are interpreted as generated from other higher-level, more abstract latents.

Image
Hierarchical Variational Autoencoder (HVAE)
We focus on a special case Markovian HVAE (MHVAE), in which each transition down the hierarchy is Markovian, where decoding each latent $z_t$ only conditions on previous latent $z_{t+1}$. Intuitively, and visually, this can be seen as simply stacking VAEs on top of each other, in a form of Recursive VAE. Mathematically, we can get the joint distribution of a Markovian HVAE and its posterior as
\[ p(x, z_{1:T}) = p(z_T)p_{\theta}(x|z_1)\prod_{t=2}^{T} p_{\theta}(z_{t-1}|z_t) \] \[ q_{\phi}(z_{1:T}|x) = q_{\phi}(z_1|x)\prod_{t=2}^{T} q_{\phi}(z_t|z_{t-1}) \]
Variational Diffusion Models: TBD